Moment of Inertia

How to calculate the moment of inertia from any axis?

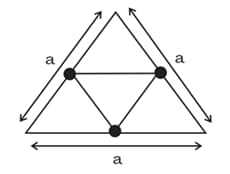
From a triangular lamina of side a and mass $m$ , a small triangular Lamina made by joining mid-points of sides of triangular lamina is cut. If Moment of Inertia of complete Lamina about COM is $I_o$ and Moment of Inertia of remaining Lamina about centroid is $\frac{x{I}_0}{16}$, then find the value of $x$.

A half section of pipe of mass $m$ and radius $r$ rests on a rough horizontal surface. Now a vertical force $F$ is applied as shown. Assuming that the section rolls without sliding. Then [Centre of mass of half ring is $\frac{2r}{\pi }$ below the centre]

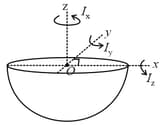
There is a uniform solid hemisphere. On its upper plane $x$ and $y$ axis are drawn which are mutually perpendicular to the upper plane and passing through the centre $O$. If moment of inertia of the hemisphere about $x,y$ and $z$-axis are $I_x,I_y$ and $I_z$ respectively then:

Four point masses $($each of mass $m$$)$ are arranged in the $X-Y$ plane. The moment of inertia of this array of masses about $Y$-axis is 

M.O.I is the ratio of 

A solid sphere, a thin ring and a cylinder of same mass and radius, held at rest are released simultaneously to roll down on an inclined plane. Which one will reach the bottom first?

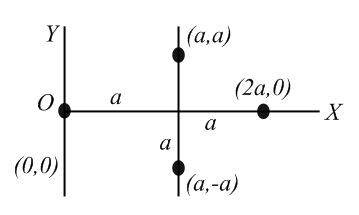
Point masses $1, 2, 3$ and $4 \mathrm{kg}$ are lying at the points $(0, 0, 0), (2, 0, 0), (0, 3, 0)$ and $(-2, -2, 0)$, respectively. The moment of inertia of this system about the $x$-axis will be,

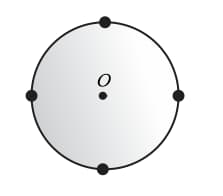
Four similar point masses (each of mass $m$) are placed on the circumference of a disk of mass $M$ and radius $R$. The moment of inertia of the system about the normal axis through the center $O$ will be,

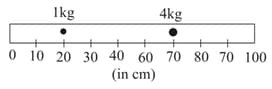
On the marks of $20 \mathrm{cm}$ and $70 \mathrm{cm}$ of a light meter scale, two weights, $1 \mathrm{kg}$ and $4 \mathrm{kg}$, respectively, are placed. The moment of inertia (in $\mathrm{kg} {\mathrm{m}}^2$) about the vertical axis through the $100 \mathrm{cm}$ mark will be,

M.O.I is the ratio of 

M.O.I. of a disc is minimum about an axis 

The parallel axis theorem uses the _____ of the distance.

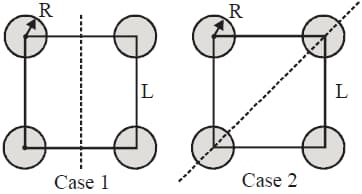
Four hollow spheres, each with a mass of $1 \mathrm{kg}$ and a radius $\mathrm{R}=10\mathrm{cm},$ are connected with massless rods to form a square with side of length $\mathrm{L}=50 \mathrm{cm},$ In case-1, the masses rotate about an axis that bisects two sides of the square. In case- 2, the masses rotate about an axis that passes through the diagonal of the square, as shown in the figure. Compute the ratio of the moments of inertia ${\mathrm{I}}_1/{\mathrm{I}}_2,$ for the two cases.

The distance in the parallel axis theorem is multiplied by _____.

The moment of inertia of a hollow cubical box of mass $M$ and side length $a$, about an axis passing through centres of two opposite faces, is equal to $\frac{xM{a}^2}{18}$. The value of $x$ is

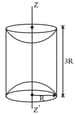
A solid cylinder is made of radius R and height 3R having mass density $\rho$ . Now two half spheres of radius R are removed from both ends. The moment of inertia of remaining portion about axis ZZ' can be calculated as $\frac{29}{6K}\pi R^5\rho$ . Find K.

A uniform thin bar of mass $6 \mathrm{kg}$ and length $2.4$ meter is bent to make an equilateral hexagon. The moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of hexagon is ________ $\times {10}^{-1} \mathrm{kg} {\mathrm{m}}^2$

A closed cylindrical container is partially filled with water. As the container rotates in a horizontal plane about a perpendicular, its moment of inertia

The inductance in a coil plays the same role as